Appunti del corso di
ECONOMIA URBANA E TERRITORIALE
PRINCIPIO DI
AGGLOMERAZIONE[1]
Andrea Rossi
Pierattilio Tronconi
Storicamente
si constata che gli uomini hanno trovato più
vantaggioso ed efficiente gestire i propri rapporti personali, sociali,
economici e di potere, in modo spazialmente
concentrato.
In uno
spazio concentrato si determinano infatti economie di
scala che consentono di sviluppare vantaggi di varia natura e di realizzare
processi produttivi più efficienti che si aggregano attorno a poli di
agglomerazione.
Il processo
cumulativo trova comunque dei limiti
a – nei costi di
trasporto, che aumentano con l’aumentare della distanza tra luogo della
produzione e luogo della commercializzazione;
b – nella formazione di diseconomie legate ai prezzi dei “fattori” meno
mobili che entrano nella produzione ed alla rendita.
I costi
di trasporto incidono nella
determinazione di quegli elementi che rendono più appetibile una localizzazione concentrata rispetto ad una diffusa.
La
rendita è connessa alla dinamica delle preferenze localizzative
delle imprese e delle famiglie.
Si
definiscono “economie di agglomerazione”
tutti i vantaggi che si possono ricavare da una “struttura spaziale
concentrata”; si tratta di:
·
economie interne alle imprese;
·
economie esterne alle imprese ma interne alle stesse
industrie o settore produttivo;
·
economie esterne alle imprese ed all’industria, connesse
all’urbanizzazione.
ECONOMIE
DI SCALA
L’area di mercato dell’impresa
La realtà mostra
che la produzione è sensibile sia ai costi di trasporto delle merci che ai
costi dei fattori produttivi i quali risultano a loro
volta sensibili alle economie di scala.
Costo del
trasporto ed economie di scala intervengono nel
determinare un modello di localizzazione delle attività produttive che viene
denominato di “diffusione concentrata” in cui sono presenti
agglomerazioni di dimensione più o meno grandi poste ad una certa distanza
l’una dall’altra.
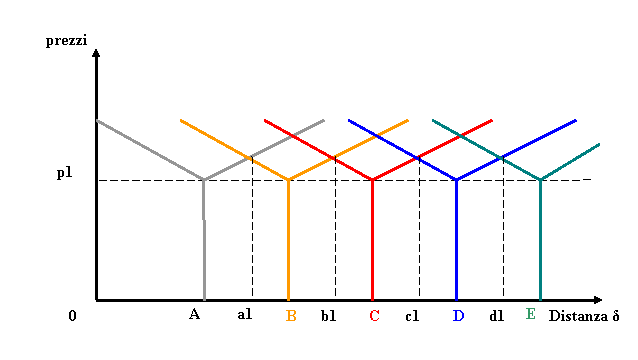
Supponendo
un mercato lineare, il grafico seguente illustra gli “spazi di mercato”
che diverse imprese (A, B, C, D,) che si trovano
distanziate tra loro e che producono con le stesse funzioni di produzione dei
beni allo stesso prezzo (p1), si troverebbero a disporre in conseguenza dei
costi di trasporto (fig 1).
La somma
del prezzo di produzione (p1) e di quello del trasporto (τ.δ),
proporzionale alla distanza (δ), rappresenta il prezzo al consumatore.
p
= p1 + (τ.δ)
|
|
Fig. 1 – aree di un mercato lineare in cui
le imprese producono tutte con lo stesso prezzo, in funzione della distanza.
L’impresa A
si troverebbe a poter occupare lo spazio compreso tra
O e a1
L’impresa B,
lo spazio tra a1 e b1
L’impresa
C, lo spazio tra b1 e c1, e così via
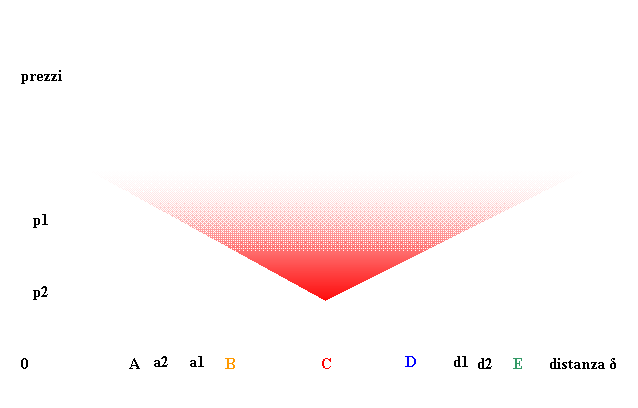
Se una
delle imprese, ad esempio la C, produce a costi minori delle altre (p2),
rimanendo costanti i costi di trasporto (τ.δ), le aree di mercato si modificherebbero come rappresentato nel grafico
seguente (Fig 1a). L’impresa C allargherebbe
il proprio spazio di mercato da (b1 – c1 di fig.1) a a2 - c2, estromettendo così le imprese B e D ed erodendo
spazi anche alle imprese A e E.
|
|
Fig. 1a - Aree di mercato in un mercato
lineare in cui una impresa produce a prezzi inferiori
rispetto alle altre, in funzione della distanza.
In un mercato
che viene dominato da una impresa ne derivano:
a – permanenza dei
vantaggi per i consumatori più vicini (minori costi di trasporto),
b – barriere spaziali alla
concorrenza,
c – possibilità di imporre
prezzi di monopolio.
LA CURVA DI
DOMANDA SPAZIALE
La domanda
spaziale indica la quantità di
beni (Xi) che un individuo è disposto
ad acquistare dall’impresa “ i ” in funzione della sua distanza (δ)
dall’impresa stessa e del prezzo complessivo (P).
Supponendo
per semplicità un mercato lineare avente come centro A (fig.2) , il prezzo complessivo di un
prodotto (P) è dato da:
P = Pf + Pt
in cui
Pf
= prezzo franco fabbrica di un lotto
x1
Pt
= prezzo del trasporto che è funzione della distanza dal luogo di produzione
Una volta noto l’andamento
del prezzo del bene P in funzione della quantità prodotta (Xi):
P = Pmax – (b) . (Xi)
in cui
Pmax
= prezzo massimo alla distanza zero dalla produzione ed a produzione minima
b =
coefficiente di elasticità del prezzo al variare delle quantità prodotte
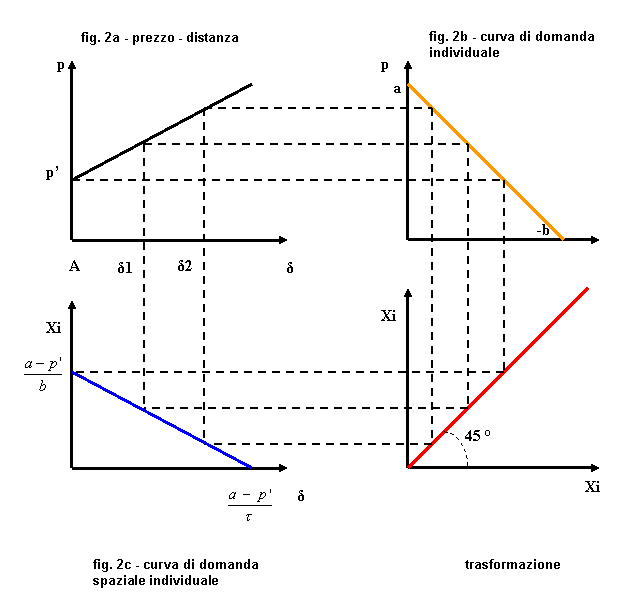
è possibile determinare la
“domanda spaziale individuale” (fig. 2)
Essendo P
= Pf + Pt (fig. 2a)
ovvero P = Pmax – b . (Xi) (fig. 2b)
si può scrivere
Pf
+ Pt = Pmax – b . (Xi)
da cui si ricava (fig. 2c)
(b) . (Xi) = Pmax - Pf – Pt
Xi
= ![]()
|
|
Xi
Fig. 2
– Costruzione della curva di domanda spaziale individuale
Se si
suppone una densità uniforme uguale a (d) consumatori per ogni unità di
distanza, la domanda complessiva risulta data
da:
a – caso del mercato
lineare, dall’area sottostante la curva di domanda spaziale
individuale (area ABO della fig.3a), moltiplicata la
densità (d)
|
|
Fig.3a - Costruzione della domanda di
mercato spaziale – Mercato lineare
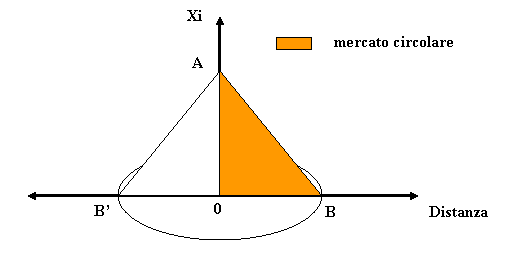
b – caso di mercato
circolare, dal volume del cono ottenuto facendo idealmente ruotare
di 360° il triangolo formato dalla curva di domanda individuale AOB (fig.2a) attorno all’asse verticale (fig.3b),
anch’esso moltiplicato per la densità (d)
|
|
Fig. 3b - Costruzione della domanda di mercato
spaziale – Mercato circolare
La fig. 2b
rappresenta anche il cono di domanda di Lösch la cui forma e dimensione dipendono,
data la struttura della domanda dei consumatori, dal costo di trasporto e dal
prezzo franco fabbrica del prodotto.
L’EQUILIBRIO
DI MERCATO E LA LOCALIZZAZIONE DELL’IMPRESA
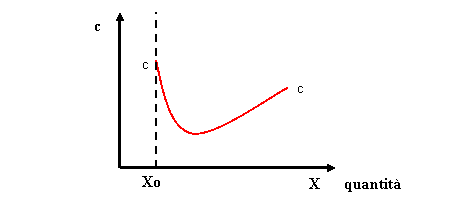
La fig. 4a
rappresenta la curva di offerta, ossia
l’andamento del costo medio (c) che una impresa incontra per realizzare
una determinata merce, in funzione delle quantità prodotte (X)
|
|
Fig. 4a
Si nota
dalla figura che l’impresa, al di sotto di una
dimensione minima di scala (Xo) non ha più
alcuna convenienza a produrre poichè i costi
diverrebbero proibitivi.
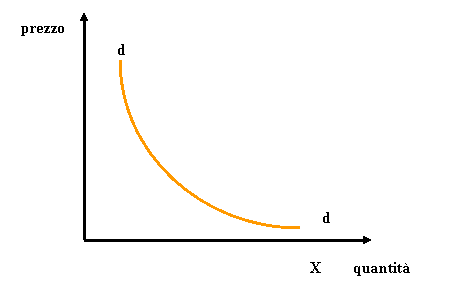
La fig. 4b rappresenta
invece la curva di domanda complessiva, ovvero l’andamento dei prezzi al
variare della quantità.
|
|
Fig. 4b
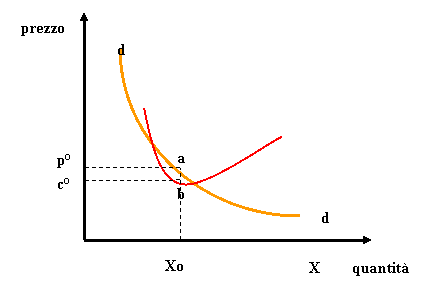
Sovrapponendo
le due curve e ricavando da esse le curve dell’offerta
marginale e della domanda marginale, l’impresa, al fine di
massimizzazione il profitto, definisce la quantità ottimale da produrre ed
il relativo prezzo (Fig.4c)
|
|
Fig.4c
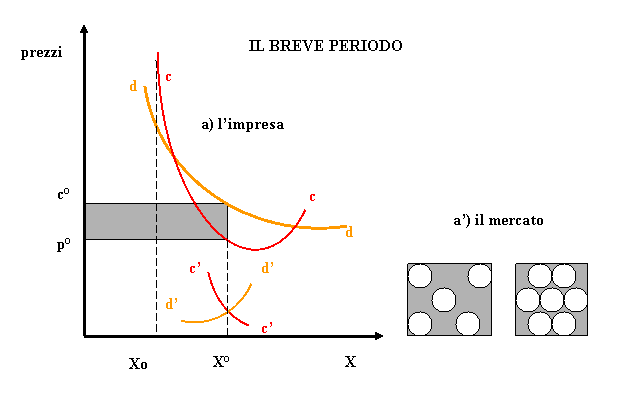
Sotto
l’aspetto spaziale, il prezzo del prodotto così definito determina un’area di
mercato dell’impresa ed una sua localizzazione tale da non sovrapporsi, nel
breve periodo, a quella di altre imprese (fig. 5a).
|
|
Fig. 5 - Equilibrio economico spaziale dell’impresa nel
breve periodo
In questa
situazione, di non equilibrio, l’esistenza di aree di
domanda non servita e di margini di sovraprofitto
attirerà nuove imprese del settore. Si determinerà così una sovrapposizione
delle rispettive aree di mercato e, di conseguenza, una diminuzione della
domanda di queste ultime ed un aumento dei loro costi.
Il margine di extra profitto precedente si ridurrà a zero e le aree di
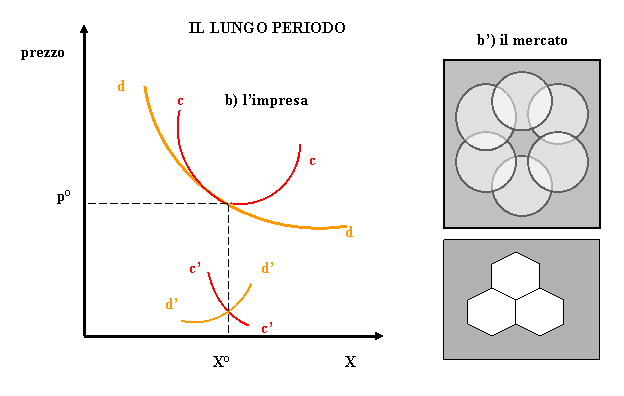
mercato tenderanno ad avvicinarsi alla forma di esagoni regolari (fig.5b). Si ricorda che l’esagono regolare è il poligono a
maggior numero di lati fra quelli che esauriscono la superficie del territorio
e pertanto rappresenta il più efficiente modo di ripartizione della superficie
stessa del territorio.
Questa
situazione rappresenta una condizione di equilibrio di
lungo periodo.
|
|
Fig. 5b - Equilibrio economico spaziale
dell’impresa nel lungo periodo
LE
ECONOMIE DI LOCALIZZAZIONE E DI URBANIZZAZIONE
Le imprese
Mentre
nelle imprese le economie interne di scala favoriscono la crescita dimensionale
dei volumi prodotti nello stesso luogo, quelle esterne favoriscono invece la
concentrazione nello stesso territorio di imprese e
attività diverse.
Per economie
di localizzazione
si intendono quelle economie connesse alla
agglomerazione di attività simili che sono esterne alle singole imprese ma
interne al settore industriale o all’industria.
Queste
economie riguardano:
a – la possibilità del costituirsi di processi di
specializzazione fra imprese all’interno del ciclo produttivo settoriale
complessivo,
b
– la riduzione dei costi di transazione all’interno dell’area e fra le diverse
unità produttive,
c
– la formazione di un bacino di manodopera specializzata,
d
– la formazione di una serie di servizi,
e
– la creazione di una cultura industriale diffusa.
Il
modello elaborato da A. Weber prevede il formarsi di una localizzazione
agglomerata delle unità produttive ogni volta che i vantaggi da essa derivanti ed i risparmi sul costo del lavoro, dovuti
alla maggiore professionalità dei lavoratori o alla maggiore disponibilità di
mano d’opera, superino i maggiori costi di trasporto connessi alla
localizzazione effettiva rispetto ad una astratta localizzazione basata sulla
minimizzazione dei costi di trasporto.
Questo
modello non è esente da forti critiche connesse al fatto che:
·
esso è
un modello statico, che ignora le dinamiche connesse ai processi evolutivi;
·
risponde
ad un approccio di equilibrio parziale, in cui non esiste interazione nei
comportamenti d’impresa;
·
rispecchia le caratteristiche essenziali di processi di
industrializzazione e urbanizzazione del secolo scorso.
Per economie di urbanizzazione
si intendono quelle economie connesse alla presenza nell’ambiente urbano di
tutte le attività economiche e non solo di singoli settori produttivi.
Queste
economie nascono a seguito:
·
della concentrazione nella città dell’intervento pubblico
sia sul versante dei consumi che degli investimenti connessi alla infrastrutturazione del territorio (sistemi di trasporto
per merci e persone, sistemi di comunicazione e informazione , ecc.);
·
della natura di vasto mercato della città;
·
dal fatto che la città è incubatrice di fattori
produttivi e di mercato degli input di produzione (lavoro altamente qualificato
e ampio, offerta di capacità direttive e manageriale, servizi alle imprese,
servizi commerciali e finanziari, ecc. ).
Le famiglie
Relativamente alle
famiglie, i fattori che spingono
all’agglomerazione sono:
·
i vantaggi connessi alla presenza di servizi pubblici
( ospedali, scuole, biblioteche, sistemi di trasporto, infrastrutture per il
tempo libero, ecc.);
·
i vantaggi derivanti dalla presenza di servizi privati
alla persona, di organizzazioni culturali, ecc.
·
i vantaggi connessi alla varietà di opzioni possibili
per quanto riguarda il lavoro, la residenza, la gestione del tempo libero, gli
acquisti, ecc.
ESISTE UNA
DIMENSIONE OTTIMA DI CITTA’ ?
Tra gli
studiosi esiste un generale consenso attorno al fatto che tutti i fattori
finora citati smettono di operare quando si superi una certa dimensione urbana.
Le economie
si trasformano infatti nel loro contrario, ossia in diseconomie.
Ad esempio superata una
certa soglia di utilizzo delle infrastrutture, il traffico urbano porta alla
congestione o ad una crescita dell’inquinamento.
I tentativi
di individuare tramite curve rappresentanti i costi ed i benefici, le
dimensioni critiche della città, si sono rivelati inapplicabili e rappresentano
per lo più delle formalizzazioni concettuali.
Oggi si
propende, più che sull’individuazione di una dimensione ottimale
di città, sull’individuazione di un intervallo di dimensioni efficienti.
Oltre alle
analisi di equilibrio parziale che prendono in
considerazione i costi e benefici della dimensione urbana, esistono anche altri
approcci che si fondano su modelli di dominazione e di rapporti monopolistici.
NOTE