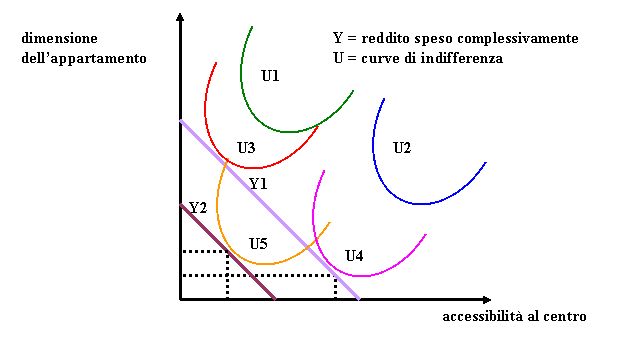Appunti del corso di
ECONOMIA URBANA E TERRITORIALE
IL PRINCIPIO DI
ACCESSIBILITA’[1]
Andrea Rossi
Pierattilio Tronconi
Il
problema dell’accessibilità dello spazio urbano nasce a seguito della
competizione che si stabilisce fra le varie attività economiche e fra queste e le famiglie al fine di
assicurarsi le localizzazioni più vantaggiose.
“Accessibilità significa superamento della barriera imposta dallo
spazio al movimento di persone e cose ed allo scambio di beni, servizi,
informazioni.” [2]
La
competizione per l’accaparramento del suolo urbano favorisce le dinamiche
connesse alla rendita fondiaria che i proprietari dei suoli esigono ed al loro
prezzo mercato.
Ai
primi dell’ottocento l’economista della scuola classica Von
Thünen elaborò un modello al fine di spiegare la
distribuzione territoriale di produzioni agricole differenti.
IL MODELLO
DI VON THÜNEN
Il
modello di Von Thünen si
fonda su una serie di ipotesi semplificatrici:
1 – una pianura omogenea con suolo di uguale fertilità e
infrastrutture di trasporto in tutte le direzioni,
2 – l’esistenza di un unico centro che funge da mercato per tutti
i prodotti che vi devono essere trasportati,
3 – disponibilità diffusa di tutti i fattori produttivi e degli
input di produzione che pertanto non devono essere trasportati,
4 – una funzione di produzione specifica per ciascun prodotto
agricolo, a coefficienti fissi e rendimenti di scala costanti,
5 – il prezzo di ciascun prodotto viene definito esogenamente su un mercato più vasto di quello in oggetto,
6 – il costo di trasporto unitario è costante, per cui esso varia
al variare dei volumi della produzione e con la distanza in modo lineare,
7 – una domanda
illimitata dei prodotti.
La
rendita per unità di superficie, conformemente alle teorie economiche
classiche, viene assunta come residuale, ossia essa è quanto rimane dopo aver
sottratto dal ricavo totale tutti i costi, comprensivi di quelli di produzione
e di trasporto e di un profitto normale.
In
particolare la rendita scaturisce dal risparmio sui costi di trasporto che il
produttore localizzato sui terreni più vicini al mercato centrale può
realizzare.
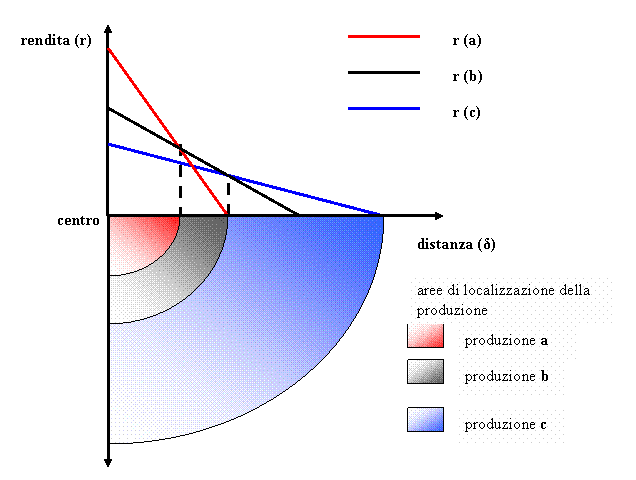
Prendendo
in esame tre tipi di colture: (a), (b), (c), Von Thünen descrive tramite un
grafico le tre curve di rendita unitaria massima che può essere pagata.
Indicando
con:
τ = il costo di trasporto unitario
δ = la distanza dal centro
x = la quantità di ciascun prodotto ottenibile su ogni unità di
terra
p = il prezzo di ciascun prodotto
c = il costo unitario di produzione
r = la rendita per unità di superficie
La
rendita per unità di superficie è una funzione della distanza ed è data dalla
seguente equazione:
r(δ) = ( p – c – τ. δ) . x (1)
Graficamente
la rendita pagabile da ciascun tipo di coltura è rappresentata da una retta
inclinata negativamente, con inclinazione pari a (–τ.x)
e da una intercetta pari a (p – c).x.
|
|
Alla
distanza massima (δ max) la rendita è
uguale a zero poichè l’insieme dei costi uguaglia il
prezzo del prodotto. Cessa così la possibilità per l’impresa di produrre quella
specifica merce.
Analiticamente,
ponendo nell’equazione (1) r = 0, si ha
(p – c ) . x = τ. δ. x
e
δ max = (p – c ) / τ
Nella competizione tra i vari settori per accedere al suolo, ogni
unità di superficie verrà attribuita a quella produzione che è in grado di
offrire la rendita maggiore.
Le tre colture si disporranno in cerchi concentrici attorno al
mercato e la rendita effettiva sarà costituita dall’inviluppo delle tre curve
di rendita offerta.
Nella
figura i terreni centrali verranno pertanto attribuiti al prodotto (a)
che presenta il più elevato prodotto netto per unità di superficie, ossia al
prodotto che utilizza il fattore terra nel modo più intensivo ed economicamente
efficiente.
LOCALIZZAZIONE
URBANA DELLE ATTIVITA’ PRODUTTIVE
Facendo
assumere al modello di Von Thünen
una valenza più generale in ambito urbano, si considera ora un una città
localizzata in uno spazio omogeneo in tutte le direzioni, privo di
caratteristiche fisiche distintive in ogni sua parte e percorribile
perfettamente in senso radiale.
Si
suppone altresì una città dotata di un centro, definito come la località più
appetibile per ogni attività economica.
Dati questi presupposti, una simile città può essere analizzata su
una sola dimensione: lungo un raggio uscente dal centro e rivolto alla
periferia.
Per
una singola impresa, la preferenza per una localizzazione centrale è espressa
dalle funzioni di costo medio complessivo per unità di produzione, incluso un
margine di profitto medio e dei costi di trasporto e di ricavo per unità di
suolo, rispettivamente crescenti e decrescenti con la distanza.
Indicando
con:
τ = il costo di trasporto unitario
δ = la distanza dal centro
x = la quantità di ciascun prodotto ottenibile su ogni unità di
terra
p = il prezzo di ciascun prodotto
z = il profitto medio
c = il costo medio complessivo per unità di produzione = z +
τ (δ)
V = ricavo totale
T = quantità di suolo richiesto
v = ricavo per unità di suolo = V / T = px
. x (δ)
r = la rendita per unità di superficie
la funzione della rendita al variare della distanza dal centro, diventa:
r(δ) = [px – z –
c(δ)] . x(δ) (2)
essa
rappresenta “l’offerta di rendita”, ossia la rendita unitaria di
equilibrio che l’impresa è disposta ad offrire alle diverse distanze dal
centro.
Nel
centro, ossia quando δ = 0 e la rendita è massima, possono ubicarsi
solo quelle imprese che, a parità di profitto unitario, possono conseguire
maggiori ricavi e/o produrre a minori costi. A distanze maggiori, l’impresa
potrà conseguire lo stesso profitto solo a condizione di offrire una rendita
minore (allontanandosi dal centro infatti aumentano i costi di trasporto).
L’inclinazione della curva di offerta di rendita è data da:
r’δ = dr/dδ = = [px
– z – c(δ)] . x’δ – c’δ
. x(δ) (3)
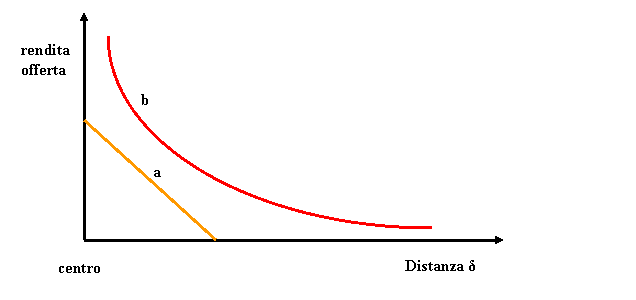
Qualora
solo i costi o solo i ricavi dipendessero dalla distanza e tale relazione
fosse di tipo lineare, la curva di offerta di rendita sarebbe rappresentata da
una retta inclinata negativamente, caso a della fig. 2.
Nel
caso in cui invece sia i costi che i ricavi dipendessero dalla
distanza, allora la curva di offerta di rendita diviene convessa e con una
pendenza decrescente con la distanza dal centro, caso b della fig. 2.
|
|
Fig. 2 – Curva di offerta di
rendita al variare della distanza dal centro relativa ad un solo livello di
profitto (z).
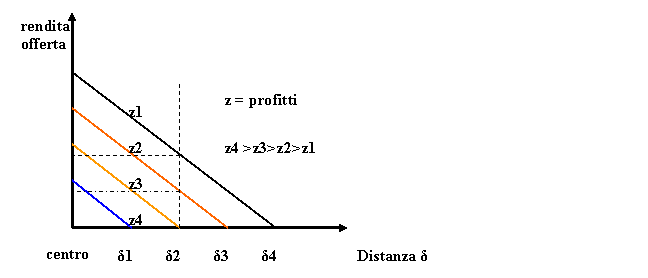
La
fig. 3 rappresenta invece la famiglia di curve di offerta di rendita al variare
della distanza dal centro per profitti costanti e crescenti verso il centro.
Ne
deriva che a parità di distanza, tenendo pertanto costanti sia le vendite che i
costi, se l’impresa vuole conseguire un maggiore margine di profitto dovrebbe
offrire una rendita minore.
Imprese
diverse, che hanno costi di trasporto con diversa incidenza o che presentano
diversi apprezzamenti della prossimità al centro, esprimono famiglie di curve
di offerta di rendita con diversa inclinazione. Quelle alle quali il centro
offre comparativamente vantaggi maggiori (esempio le imprese connesse alle
attività terziarie) presentano curve maggiormente inclinate.
|
|
Fig. 3 – Famiglia di curve di offerta di rendita nel
caso lineare e con profitti crescenti verso il centro.
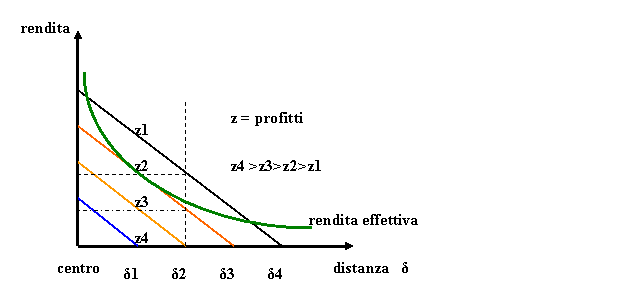
In un approccio di equilibrio parziale, la localizzazione ottimale
dell’impresa è ottenuta introducendo esogenamente la
curva di rendita effettiva,
espressiva dei valori riscontrabili sul mercato. L’impresa potrà così
scegliere, tra le varie opzioni, la localizzazione che le consentirà di
ottenere il profitto più elevato. Esso è rappresentato dal punto di tangenza
con la curva di offerta (fig.3).
|
|
Fig. 4 – Equilibrio localizzativo (caso lineare).
Dall’equazione
(4) è possibile ricavare una tassonomia semplificata delle attività che hanno
una elevata attrazione per il centro (che pertanto esprimono la maggiore
inclinazione della curva).
|
c’δ |
x’δ |
x |
(p-z-c) |
Attività |
|
= 0 |
Elevato |
Normale |
Normale |
Orientate alla densità della domanda centrale (commercio) |
|
= 0 |
Elevato |
Normale |
Elevato |
Orientate all’informazione (finanza, giornali, terziario
professionale) |
|
= 0 |
Normale |
Normale |
Elevato |
Orientate ai simboli del potere (oligopoli privati e monopoli
pubblici) |
|
> = 0 |
Normale |
Elevato |
Elevato |
Alta efficienza spaziale (attività telematizzate) |
|
> 0 |
= 0 |
Normale |
Normale |
Servizi banali alle attività centrali |
|
> 0 |
= 0 |
Normale |
Elevato |
Servizi avanzati che usano infrastrutture centrali
(spedizionieri) |
Tab. 1 – Tassonomia delle
attività a vocazione centrale [ricavata da [3]].
LOCALIZZAZIONE
URBANA DELLE ATTIVITA’ RESIDENZIALI
Il
principio di accessibilità si applica anche alle attività residenziali dato che
il centro esercita una forte attrazione per le opportunità che in genere offre.
La
propensione verso localizzazioni centrali da parte di vari soggetti (imprese,
individui) sviluppa una concorrenza che incide sul livello dei prezzi delle
aree relative e dei livelli della rendita urbana.
La
scelta della localizzazione residenziale dovrà pertanto essere effettuata
tenendo conto del differenziale dei costi da sostenere tra centro e periferia
connessi alla rendita (fig.2) e rapportando i costi
sostenibili con i vantaggi conseguibili (ad esempio minori spese di trasporto)
per le varie localizzazioni.
Poichè i costi residenziali non sono solo connessi alla localizzazione
ma anche alla dimensione dell’appartamento, ne deriva che una volta definito il
reddito che si ritiene di spendere, è possibile ripartire tale spesa tra i
costi connessi alle dimensioni dell’appartamento e quelli derivanti dalla
localizzazione. La scelta del punto di equilibrio si esercita in base alla
struttura della funzione individuale di utilità, evidenziata
dalla forma ad U delle curve di
indifferenza (fig.5).
|
|
Fig. 5 – Trade – off
accessibilità – dimensione dell’appartamento (a parità di reddito speso in casa
+ trasporti).
All’aumentare
del reddito speso complessivamente (da Y1 a Y2), gli individui che esprimono la
famiglia di curve di indifferenza più basse (U2 e U4) e per i quali
l’accessibilità al centro costituisce un bene “superiore”, tenderanno a
privilegiare quest’ultimo anche a costo di una
riduzione delle dimensioni dell’appartamento.
Al
contrario gli individui che esprimono la famiglia di curve di indifferenza più
alte (U1, U3, U5), per i quali il bene superiore è rappresentato dalle
dimensioni dell’appartamento, privilegeranno questa opzione rispetto
all’accessibilità.
La
decisione localizzativa verrà effettuata ottimizzando
il trinomio:
accessibilità – costo dell’area –
dimensione dell’unità residenziale
Assumendo
sempre il fatto che un individuo effettui le proprie scelte su una base di razionalità
economica dettata dalla ottimizzazione della relazione costi - benefici e non
considerando la dimensione dell’unità di residenza, costui, definito il reddito
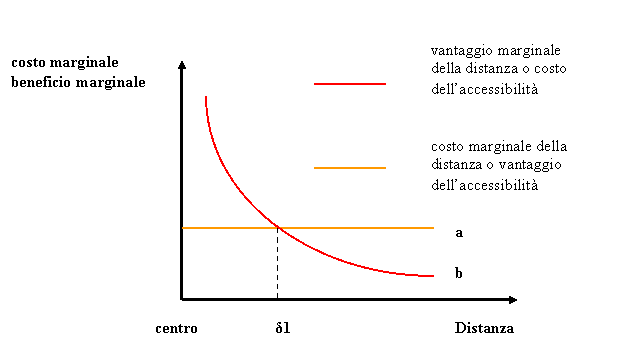
spendibile, sceglierà (Fig. 6) quella distanza dal
centro (δ1) in cui il costo marginale di un ulteriore spostamento
verso l’esterno (retta a) eguaglia il vantaggio derivante dal risparmio
sul costo dell’area (curva b).
|
|
Fig. 6 – Decisione localizzativa a parità di dimensione dell’appartamento.
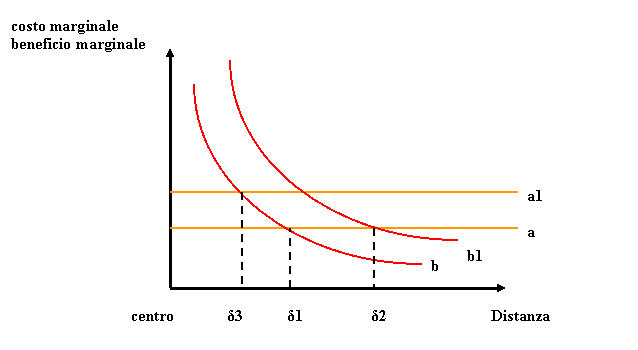
Se
a seguito di un aumento del reddito e quindi della capacità di spesa,
l’individuo ritenesse di passare al bene superiore dato dalla dimensione
dell’appartamento, la curva (b) dei costi dell’accessibilità si
sposterebbe verso l’alto (b1) e la localizzazione si sposterebbe verso
l’esterno da (δ1) a (δ2) (fig.7).
Se
invece venissero privilegiati vantaggi derivanti dall’accessibilità una
localizzazione più centrale passando da una curva (a) a (a1) il
punto di intersezione si sposterebbe in (δ3).
|
|
Fig. 7 – Effetto di un aumento del reddito
disponibile sulla localizzazione.
OSSERVAZIONI
AI MODELLI DI LOCALIZZAZIONE URBANA
I
modelli di localizzazione urbana produttiva e residenziale sopra descritti,
sono modelli di equilibrio parziale in quanto definiscono le decisioni localizzative ottimali per il singolo soggetto (impresa o
individuo) nell’ipotesi che tutti
gli altri soggetti abbiano già trovato una localizzazione che non intendono
modificare in conseguenza delle decisioni del soggetto in esame.
I
modelli presuppongono che sia data esogenamente una
curva di rendita effettiva.
Questo
approccio fa emergere degli interrogativi circa:
·
la
localizzazione di tutti gli altri soggetti che hanno le stesse caratteristiche
dei soggetti singolarmente esaminati, visto che non è possibile che tutti si
localizzino nelle stesso spazio o alla stessa distanza dal centro;
·
il
modo di localizzarsi di settori diversi o di individui aventi redditi e
preferenze diverse.
Per
tentare di formulare delle risposte a tali problemi, si richiedeva il passaggio
da modelli di equilibrio parziale a modelli di equilibrio generale, in
cui la curva di rendita effettiva non è più data esogenamente
ma viene costruita direttamente dal modello stesso.
Facendo
riferimento alle localizzazioni produttive, la risposta al primo
problema viene data assumendo come dato il saggio di profitto comune.
Ne
deriva che imprese diverse ma simili, che esprimono un’unica curva di offerta
di rendita, si disporranno lungo tale curva a distanze diverse dal centro. La
curva di rendita offerta diviene così la curva di rendita effettiva ed il suo
andamento, che non è rettilineo, assume la forma di iperbole (curva b
della Fig.2).
Avvicinandosi al centro, il problema della scarsità di terra e dei
relativi costi elevati viene affrontato costruendo in altezza; ciò porta ad una
crescita della densità d’uso del suolo che varia in diminuzione man mano che si
va dal centro alla periferia . La città assumerà al centro un profilo
verticale.
Qualora
i settori fossero più di uno, essi si localizzeranno lungo l’inviluppo
superiore delle rispettive curve di rendita offerta, come nel modello di Von Thünen.
Per
quanto riguarda le localizzazioni residenziali, si ipotizza che sia dato
il livello di utilità raggiungibile da tutti gli individui, aventi lo
stesso reddito e struttura di preferenze, che si trovano a consumare
entro un mercato in cui sono presi in considerazione tutte le merci
acquistabili e la quantità del suolo abitabile.
Data
questa premessa, gli individui definiscono come spendere il proprio reddito (
tra merci e residenza) e con ciò anche il massimo livello di rendita pagabile
alle varie distanza dal centro. E’ allora possibile costruire una famiglia di
curve di rendita offerta corrispondenti ai livelli possibili di utilità.
Il
modello può essere elaborato ipotizzando la dimensione demografica della città (modello
della città chiusa) ed assumendo esogenamente il
livello della rendita al margine della città pari al livello della rendita
agricola (livello minimo della rendita).
Un
altro modo di elaborazione del modello prevede invece di assumere come incognita la popolazione
della città (modello della città aperta) per cui sono resi possibili i
movimenti migratori di individui sulla base delle varie classi di reddito e di
un confronto di utilità tra localizzazioni diverse. In questo caso il livello
di utilità di una localizzazione urbana è dato esogenamente
ed assunto uguale a quello generale, nazionale.
L’esistenza di classi di reddito diverse darebbe luogo a
formazioni di città che si configurerebbero come anelli concentrici con al
centro la classe più agiata.
In
cui in ciascun anello risiederebbero, in equilibrio di indifferenza localizzativa, i membri di ciascuna classe.
Qualora
il problema dell’accessibilità venga trattato considerando la presenza
contemporanea delle due domande (delle imprese e degli individui), il
modello mostra che la terra urbana verrebbe ad essere assegnata sempre sulla
base della capacità di offerta di
rendita.
In
genere si rileva che le attività economiche, in particolare quelle legate al
terziario ed alle funzioni direzionali, potendo pagare rendite cospicue,
spiazzano la domanda residenziale dalle aree centrali.
Le
attività manifatturiere, necessitando di grandi spazi, tenderanno a disporsi
alla periferia.
Applicando il modello della “città aperta” su scala nazionale,
ossia su un territorio in cui sono uguali i livelli di utilità e le funzioni di
produzione, si otterrebbero città aventi la stessa dimensione.
La
realtà però mostra una situazione alquanto diversa dato che coesistono, accanto
a città di grande dimensione, città di media e piccola dimensione.
In
conclusione si può osservare che:
a
– le economie di agglomerazione derivanti dall’assunzione di criteri di
perfetta razionalità economica e, tra questi, l’ipotesi di assegnare al costo
del trasporto un ruolo centrale e determinante, non spiegano la struttura reale
dei movimenti pendolari e della domanda di trasporto che ne deriva. La volontà
di limitare i costi di trasporto verso il centro rappresenta infatti una delle
molteplici variabili che condizionano le scelte di localizzazione delle imprese
e degli individui;
b
– nel caso di “molte città” il modello genera, in equilibrio, una struttura
urbana formata da città aventi la stessa dimensione, fatto che non trova
riscontro nella realtà. Per ovviare a questo inconveniente occorrerebbe introdurre
nel modello altre ipotesi che però contrasterebbero con la logica economica
stessa del modello, ossia l’assunzione di un equilibrio spaziale perfettamente
competitivo basato sulla sola sostituibilità fra accessibilità fisica e
disponibilità di beni (per il consumatore) o sulla sostituibilità fra terra e
capitale (per il produttore). [(1) pag.92];
c
– il modello, simulando una “città istantanea”, in cui tutte le attività,
perfettamente mobili, vengono ad allocarsi simultaneamente nello spazio urbano,
è strutturalmente statico.
IL MODELLO
DELLA SCUOLA DI CHICAGO E DI HOYT
I
modelli di localizzazione sin’ora esaminati, basati
sul principio dell’accessibilità, mostrano che le città si strutturerebbero in
forma circolare per anelli concentrici attorno al punto di massima attrattività. Partendo da altri assunti derivati dalla sociologia
urbana, la scuola di Chicago ha elaborato negli anni venti un
modello da cui emerge una struttura di città che tende ad espandersi in senso
radiale per cerchi concentrici attorno al centro degli affari.
Andando
verso la periferia si trovano:
·
zone
caratterizzate da presenza di uffici e industria leggera, inframezzate
da aree degradate;
·
una
zona di residenza dei lavoratori qualificati e delle classi medio basse uscite
dalla zona degradata e con necessità di facile accesso ai luoghi di lavoro;
·
una
zona residenziale per classi a reddito medio alto;
·
una
zona esterna di pendolarismo.
L’espansione della città è determinata dalle dinamiche interne di spiazzamento successivo derivanti dalla competizione fra
usi alternativi del suolo, per cui ogni zona tende a espandersi e ad invadere
la zona successiva.
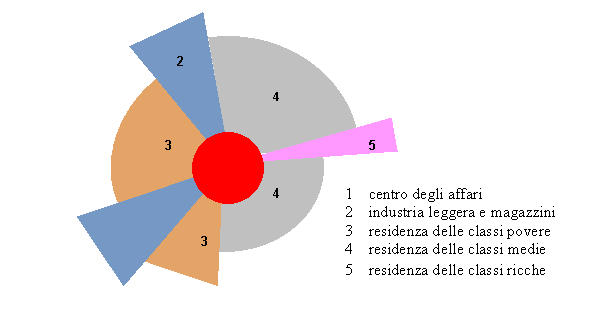
Hoyt, assumendo una posizione critica nei
confronti del modello della scuola di Chicago, ha proposto un modello in cui
la città tende a strutturarsi sempre in senso radiale ma in settori circolari a
forma di cono.
Hoyt
osserva infatti che in realtà i singoli settori o tipologie residenziali non si
sviluppano su cerchi, come se la distanza da un unico centro rappresentasse il
solo fattore di organizzazione spaziale, ma si concentrano in aree specifiche a
seguito della attrattività e repulsione fra settori e
attività diverse (Fig.8).
|
|
Fig. 8 – Strutture urbana secondo Hoyt.
NOTE