|
L’organizzazione spaziale della città RANK-SIZE RULE[1]Teorie e metodi per l'analisi dei sistemi territoriali e urbani Appunti delle lezioni del corso di Analisi dei sistemi urbani e territoriali C.Prof. Ferdinando Semboloni Per analizzare la organizzazione di un insieme di centri urbani si studia la distribuzione della popolazione tra i centri. Per fare questo si stabiliscono delle classi di ampiezza demografica e per ogni classe si conta il numero dei centri urbani che vi ricadono. Questo numero, come abbiamo visto nel capitolo dedicato ai richiami di statistica si chiama frequenza. Se si fa la stessa cosa considerando la statura di un certo numero di persone si troverà probabilmente una distribuzione simmetrica intorno alla media: molti individui avranno una altezza simile a quella media, un numero minore avrà una altezza superiore o inferiore alla media. In generale la distribuzione delle popolazione tra le città non è simile a quella precedentemente citata. Difatti la distribuzione di centri urbani è tale per cui si hanno poche città grandi e molte città piccole. In altre parole, se si fa un esperimento simile a quello fatto con la statura delle persone si troverà una quantità alta di casi a sinistra della media ed una quantità esigua a destra. Difatti la legge che lega frequenza e dimensione delle città è una legge cosiddetta a potenza (power law). In generale invece di stabilire delle classi si ordinano le città secondo la dimensione. La città più grande è la prima della lista, la seconda è quella con popolazione immediatamente inferiore e così via. In questo caso la legge detta appunto rank-size (rango-dimensione) lega la popolazione di una città classificata ad un certo livello col livello stesso e la popolazione della città maggiore, cioè di rango 1. La equazione che lega la dimensione urbana col suo rango è la seguente:
dove Allo scopo di rendere più flessibile la legge e di renderne possibile la stima sui dati reali, viene aggiunto un parametro:
è evidente che, implicitamente nella precedente equazione si era assunto q = 1. Questo parametro rappresenta il grado di gerarchizzazione dell'insieme dei centri considerato. Questa legge la si riscontra quando si hanno condizioni equilibrate di sviluppo, senza cioè grandi differenze di reddito tra aree geografiche e quando l'area presa in considerazione è congruente con la dimensione della città più grande. Difatti, nel primo caso la differenza di reddito crea un forte disequilibrio e quindi la crescita di una città non è dipendente dal suo hinterland, ma da altri fattori. Nel secondo caso è chiaro che prendendo un'area troppo piccola posso avere al suo interno una città che serve un'area più vasta e quindi con dimensioni che non sono spiegate dalla dimensione dell'area considerata. Inoltre ci sono due problemi relativi alla grande e alla piccola dimensione. Il primo fa riferimento al fatto che spesso un centro di grandi dimensioni deborda dai propri confini amministrativi, in relazione ai quali generalmente si rileva la popolazione, rendendo difficile stabilire la sua popolazione reale. Si consideri il caso di Roma con un vasto territorio comunale in confronto con quello di Milano con un territorio ristretto in relazione alla dimensione della agglomerazione. In questi casi l'unico criterio valido per stabilire i confini di una città rimane quello della contiguità dell'edificato. Nel secondo caso l'unità di rilevamento stabilisce una maglia minima che non tiene conto delle ulteriori suddivisioni al suo interno, falsando quindi i risultati nella coda delle città ordinate per dimensione. La spiegazione della rank-size rule è stata cercata in molte maniere. In sostanza si ammette che essa sia il risultato di una interazione tra forze che tendono alla concentrazione e forze che tendono alla dispersione delle attività sul territorio.[2] [11] Le forze che tendono alla concentrazione dipendono principalmente dalla necessità di limitare i costi di trasporto e dalle economie di scala o di agglomerazione. Le forze che tendono alla dispersione dipendono principalmente dal prezzo dei beni che è più basso nelle aree dove vi è una minor domanda, o da risorse decentrate come il terreno agricolo. La tensione dinamica esistente tra queste due forze determina il risultato. Recentemente i fenomeni che assumono nel lungo periodo una distribuzione del tipo rank-size sono stati compresi nella classe della Self Organized Criticallity, in acronimo SOC. La SOC studia fenomeni che ad un certo punto del loro sviluppo si stabilizzano in uno stato che mostra una forma mediamente stabile ma soggetta a modificazioni e queste modificazioni assumono una distribuzione del tipo a potenza. I terremoti ad esempio mostrano questa distribuzione e quindi l'equilibrio raggiunto dalla crosta terrestre sarebbe del tipo SOC. L'esempio sperimentale del mucchietto di sabbia con le valanghe rappresenta bene questa situazione. Il caso delle città è un pò diverso dato che non sono i mutamenti ad assumere la distribuzione a potenza, ma piuttosto il loro accumulo in determinati punti dello spazio. Probabilmente si giungerà ad unificare questi due punti di vista. Per ora si consideri una spiegazione più semplice, di carattere statico. Essa in sostanza lega il fenomeno alla sua localizzazione nello spazio e al modo in cui le città si insediano in un territorio. Si consideri quindi un quadrato al cui centro metto una città. La città si localizza al centro perché in quel punto minimizza la somma delle distanze da tutti i punti del suo territorio. Si suppone che la città abbia una popolazione proporzionale alla estensione del territorio e alla popolazione delle città che in esso sono localizzate. In questo primo passo la popolazione della città maggiore P0 è:
Se dividiamo il quadrato in quattro, otteniamo dei quadrati nei quali si può ripetere la operazione. Avremo che la popolazione di queste città P1 è data da
e
Ripetendo la operazione per l'hinterland delle 4 città P1, ottengo quattro città P2
Generalizzando si ottiene questa serie di equazioni:
Per ogni livello avrò questo numero di città:
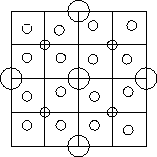
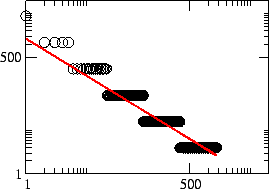
Nella figura 6.1 è schematizzata la organizzazione spaziale dei centri. Se si calcolano queste popolazioni e si mettono in ordine le città si ottiene il seguente il grafico in figura 6.2.
Come si vede, nella rappresentazione in coordinate logaritmiche la distribuzione delle città è a scalino. Tuttavia il loro andamento si avvicina a quello di una retta. Difatti se applico il logaritmo ottengo la seguente equazione:
Questa equazione è una equazione lineare e i coefficienti possono essere calcolati con il metodo dei minimi quadrati, una volta trasformati i dati nella scala logaritmica. Nel caso precedente la retta di regressione stimata è in rosso. La equazione stimata della rank-size è la seguente:
Dal momento che la inclinazione della retta mi da il grado di gerarchizzazione dell'area, più grande è il valore di q e maggiore è il grado di gerarchizzazione. Valori di q di poco inferiori a 1 sono la norma. Per inciso si noti come la costruzione di questo teorico sistema urbano è simile a quella di un albero in cui aggiungo un ramo che, pur essendo di dimensione ridotta rispetto a quella dell'albero ha una forma simile, al quale ramo aggiungo un ramo più piccolo ma sempre della stessa forma e così via. Questo tipo di crescita produce forme dette frattali che hanno la caratteristica di mantenere sempre la stessa forma (evidentemente solo i caratteri principali di essa) anche cambiando la scala. (il cavolo romano ne è un classico esempio). Queste forme producono un meccanismo di crescita detto allometrico perché la crescita di una parte è sempre proporzionale alla crescita del tutto. Ci si può chiedere perché, quando ho già una città su un territorio ho la necessità di averne una più grande che serve sia il territorio che le più piccole. Questo problema è affrontato dalla central place theory, introducendo beni con soglia variabile. NOTE |
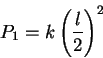
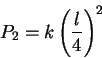
![\begin{displaymath}P_n=k \left[ \left( \frac{l}{2^n}\right)^2 +4P_{n+1} \right]\end{displaymath}](Semboloni_Ferdinando_-_ST_-_Rank-size_rule_file/image008.gif)
![\begin{displaymath}P_n=k \left[ \frac{l^2}{2^{2n}} +4P_{n+1} \right]\end{displaymath}](Semboloni_Ferdinando_-_ST_-_Rank-size_rule_file/image009.gif)