Appunti del corso di
ECONOMIA URBANA E TERRITORIALE
IL PRINCIPIO DI
COMPETITIVITA’1
LA BASE ECONOMICA URBANA
Andrea Rossi
Pierattilio Tronconi
Partendo da
una distinzione tra funzioni che si svolgono nelle città, ossia quelle che si
rivolgono ad una DOMANDA ESTERNA e quelle che invece si rivolgono a soddisfare
i BISOGNI DELLA POPOLAZIONE RESIDENTE.
Le funzioni
rivolte al soddisfacimento della domanda esterna plasmano le caratteristiche
specifiche della città, la sua specializzazione ed il suo ruolo nella divisione
spaziale del lavoro.
Sombart definisce le prime
come “attività di base” e le seconde “attività di complemento”.
Dall’assunzione
di questo punto di vista sono stati elaborati dei modelli per effettuare
previsioni di sviluppo aggregato nel breve e medio termine.
Questi
modelli non si rivolgono alla struttura delle localizzazioni delle diverse
attività nella città, ma solo alla DIMENSIONE ed alla DINAMICA QUANTITATIVA di
queste attività, aggregate in pochi settori.
La città
viene osservata come una grande macchina per produrre in cui la necessità di
importare TUTTI I BENI PRIMARI, per definizione esclusi da una produzione
urbana, e la impossibilità di produrre tutta la gamma dei beni e dei servizi, a
causa delle ridotte dimensioni del mercato sia dei beni che dei fattori, fanno
sì che per la città le ESPORTAZIONI NON SIANO UN FATTO CASUALE, MA UN ELEMENTO
NECESSARIO.
Si dà per
IMPLICITO il fatto che per esportare la città raggiunga rilevanti livelli di
COMPETITIVITA’ ESTERNA che può essere raggiunta:
a – attraverso la
specializzazione nelle funzioni caratteristiche del proprio livello gerarchico;
b –
attraverso la specializzazione su alcuni beni;
c –
attraverso specifici processi di integrazione fra industria e terziario
produttivo;
d –
attraverso processi di integrazione orizzontale o verticale
Assunta per
ipotesi l’esistenza nella città di fattori che producono “competitività esterna”
ne consegue che “le attività di base”, che lavorano per il mercato esterno,
divengono il MOTORE DELLA DINAMICA URBANA.
Dalla loro
crescita dipende infatti non solo l’OCCUPAZIONE ed il REDDITO di chi vi lavora,
ma anche, per effetto dei meccanismi vari di interdipendenza nella produzione e
nei consumi, l’OCCUPAZIONE ED IL REDDITO DELLE ATTIVITA’ COLLEGATE, a monte
delle attività di esportazione, nonchè l’occupazione
ed il reddito delle ATTIVITA’ DI SERVIZIO che si rivolgono alla popolazione
urbana complessiva.
Se la
dinamica della domanda di uno specifico prodotto di specializzazione, può
spiegare i fenomeni di sviluppo territoriale nel BREVE PERIODO, ESSA TUTTAVIA
NON RIESCE A FORNIRE SODDISFACENTI SPIEGAZIONI NEL MEDIO LUNGO PERIODO.
E’ vero
infatti che lo sviluppo di una città specializzata nella produzione di
automobili dipende dalla crescita del mercato mondiale delle automobili
(domanda in espansione), ma ciò vale solo nel breve medio periodo dato che nel lungo periodo
vengono in evidenza la capacità di sostituire nuove produzioni a quelle
eventualmente declinanti (domanda di sostituzione) nonchè
la capacità di innovazione continua del prodotto e di rilancio della
competitività internazionale della città.
Nell’analisi
dei fenomeni di sviluppo locale, all’approccio basato sulla DOMANDA, si
sono quindi sostituiti approcci centrati invece sull’OFFERTA, in
cui, per l’appunto, la qualità dei fattori produttivi, le sinergie
intersettoriali ed economiche di agglomerazione, il progresso tecnico e le
capacità innovative sono visti come i VERI ELEMENTI su cui si fonda la
COMPETITIVITA’e, quindi, la capacità di SVILUPPO DI LUNGO PERIODO DI UN ’AREA
METROPOLITANA.
In questa
nuova ottica il settore RESIDENZIALE o dei SERVIZI viene ad assumere un ruolo
ATTIVO di pre - condizione delle esportazioni stesse.
IL MODELLO
DI BASE URBANA DI HOYT (ANNI 30)
Hoyt, nella ricerca di un
metodo semplice di definizione delle prospettive di sviluppo delle città
americane, distingueva l’OCCUPAZIONE URBANA TOTALE (Lt)
in:
·
OCCUPAZIONE DI
BASE (Lb)
·
OCCUPAZIONE NON
DI BASE o di SERVIZIO (Ls)
l’occupazione
totale è data dalla somma delle due citate forme di occupazione, ossia:
Lt = Lb
+ Ls
ponendo Lb = ![]()
ed
esprimendo l’occupazione non di base come una quota (b) dell’occupazione urbana
totale:
Ls = b
. Lt in
cui 0 < b <1
sostituendo e raccogliendo avremo
Lt = ![]() + bLt
+ bLt
Lt – bLt
= ![]()
Lt (1-b) = ![]()
da cui
Lt = ![]() .
. ![]()
e in
termini di variazioni:
DLt = D![]() .
. ![]()
il fattore ![]() viene considerato come
il MOLTIPLICATORE dell’OCCUPAZIONE
viene considerato come
il MOLTIPLICATORE dell’OCCUPAZIONE
URBANA
attivato dalla dinamica della OCCUPAZIONE DI BASE.
Similmente,
introducendo un TASSO DI ATTIVITA’ (1/a ) è possibile stimare la POPOLAZIONE
(P) sulla base della OCCUPAZIONE TOTALE (Lt):
P = a . Lt in
cui a >= 1
e
riformulando l’occupazione non di base (Ls) come una
quota (b) della popolazione totale:
Ls = b
. P in cui
0 < b < 1
si ottiene
P = ![]() .
. ![]()
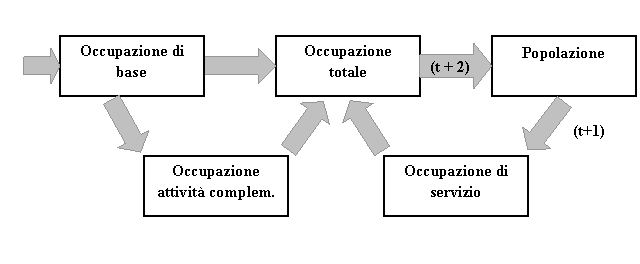
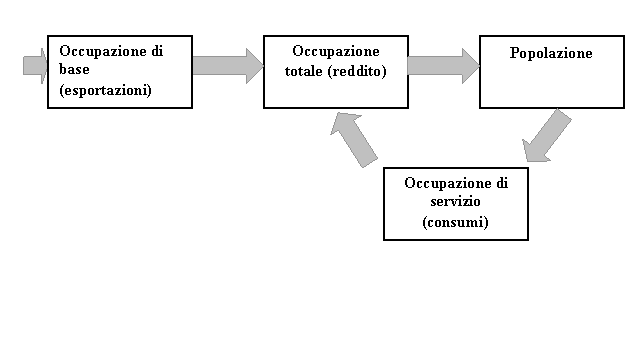
la logica
del modello di base di esportazione è schematizzata nella seguente figura.
IL MODELLO
CON VARIABILI RITARDATE DI CZAMANSKI
Czamansky propone un
modello di base economica che introduce, accanto alle tradizionali attività di
base (Lb) e di servizio (Ls)
introduce le ATTIVITA’ COMPLEMENTARI ALLE FUNZIONI DI BASE (Lc)
e stima i ritardi temporali con cui le relazioni nel modello si realizzano.
Il modello
è basato sulle seguenti equazioni:
P(t) = a1 +
b1 . Lt (t -x)
ricavando Lt (nell’ipotesi di astrazione dei ritardi temporali x ),
si ha:
Pt –a1 = b1 . Lt
Lt = ![]()
si ricorda
altresì che sulla base della nuova ipotesi, l’occupazione totale Lt è data dalla somma dell’occupazione dei tre settori,
ossia
Lt = Lb
+ Lc + Ls
esprimendo
l’occupazione connessa alle attività complementari alle funzioni di base (Lc) come una quota (b2) dell’occupazione delle tradizionali
attività di base (Lb), si ha:
Lc = a2 + b2 . Lb
e
l’occupazione connessa alle attività di servizio (Ls)
come una quota (b3) della popolazione (P), si ha :
Ls = a3 + b3 . Pt
sostituendo
Lc ed Ls alla equazione che dà l’occupazione totale (Lt) ed astraendo dalla struttura dei ritardi, si ha
Lt = Lb + a2 + b2 . Lb + a3 + b3 . Pt
raccogliendo:
Lt = Lb
(1 + b2) + a2 + a3 + b3 .Pt
sostituendo
a Lt l’equazione che esprime l’occupazione totale in
funzione della popolazione, si ha:
![]() = Lb
(1 + b2) + a2 + a3 + b3 .Pt
= Lb
(1 + b2) + a2 + a3 + b3 .Pt
operando si
ha:
Pt – a1 = b1.
Lb (1 + b2) + b1 .a2 + b1 .a3 + b1 .b3 .Pt
raccogliendo
Pt – b1 . b3 Pt = a1 + b1. Lb (1 + b2) + b1 . (a2 + a3)
Pt (1 – b1 b3) = a1 + b1. Lb (1 +
b2) + b1 . (a2 + a3)
da cui si
ricava la popolazione totale:
Pt = ![]()
Il modello
viene utilizzato per effettuare previsioni di CRESCITA URBANA sulla base della
consistenza futura di Lb
La logica
del modello è schematizzata come segue:
|
|
MODELLO
KEYNESIANO
EXPORT – LED
Tiebout e North formulano una versione del modello di base economica
sulla base di un semplice moltiplicare keynesiano del
reddito attivato dalle esportazioni.
Ipotizzando
nulle le scorte, detti:
Y = il
prodotto interno (reddito)
C = la
domanda di consumo (finale+investimenti)
E = le
esportazioni
M = le
importazioni dell’area urbana
il modello
di equilibrio è il seguente:
prodotto interno + importazioni = domanda di consumo
+ esportazioni
Y + M = C + E
Il PRODOTTO
INTERNO (Y ) è pertanto dato da
prodotto interno = domanda di consumo + esportazioni
- importazioni
Y = C + E – M
esprimendo
la domanda di consumi C come quota (c) del reddito (Y)
C = cY in
cui 0< c <1
fissate le
esportazioni
E = ![]()
ed
esprimendo anche le importazioni come una quota (m) del reddito (Y), si ha
M = mY in
cui o < m <1; m < c
sostituendo
le nuove espressioni di C, E, M nella equazione di equilibrio, si ottiene:
Y = cY + ![]() - mY
- mY
Y – cY + mY
= ![]()
Y (1 – c +
m) = ![]()
Y = ![]()
![]() in cui
0< (c-m) < 1
in cui
0< (c-m) < 1
poichè :
c =
propensione media al consumo
m =
propensione marginale all’importazione
ne deriva
(c – m) =
propensione a consumare beni prodotti internamente
Il termine ![]() è il MOLTIPLICATORE Keynesiano delle esportazioni.
è il MOLTIPLICATORE Keynesiano delle esportazioni.
Esso ci dice
che il REDDITO COMPLESSIVO è un MULTIPLO DELLA DOMANDA DI ESPORTAZIONE.
IL MODELLO
INPUT – OUTPUT
Il modello
input – output si basa sul modello delle interdipendenze settoriali elaborato
da Leontief.
Esso viene
utilizzato per la descrizione della struttura dell’economia della città e per
effettuare previsioni a breve e medio termine.
Il modello
viene limitato a due soli settori produttivi.
Il modello
è strutturato secondo una matrice quadrata n x n in cui si considerano i FLUSSI
DELLE VENDITE (sulle righe) e di ACQUISTO (sulle colonne) che si manifestano
ANNUALMENTE fra gli n settori produttivi locali.
Le somme
dei valori di OGNI RIGA che rappresentano i RICAVI TOTALI per ogni settore,
EGUAGLIANO le somme dei VALORI PER COLONNA che rappresentano l’INSIEME DEI
COSTI (comprensivi dei profitti)
|
|
settori acquirenti |
A |
B |
C |
totale |
|
settori venditori |
|
acquisti (costi) |
acquisti (costi) |
acquisti (costi) |
acquisti (costi) |
|
A |
vendite (ricavi) |
0 |
4 |
4 |
8 |
|
B |
vendite (ricavi) |
6 |
0 |
4 |
10 |
|
C |
vendite (ricavi) |
2 |
6 |
0 |
8 |
|
totale |
vendite (ricavi) |
8 |
10 |
8 |
26 |
La matrice
viene completata da una serie di colonne che presentano le vendite
settoriali ALLA DOMANDA FINALE e da una serie di righe che presentano le
diverse componenti del VALORE AGGIUNTO SETTORIALE (SALARI E PROFITTI) e le
IMPORTAZIONI.
La somma
delle componenti della DOMANDA FINALE (NELL’ESEMPIO 51) EGUAGLIA la SOMMA DELLE
COMPONENTI DEL REDDITO O DI VALORE AGGIUNTO E DELLE IMPORTAZIONI.
|
domanda intermedia |
domanda finale |
|
|||||||
|
|
settori acquirenti |
A |
B |
C |
consumi privati |
consumi pubblici |
investimenti |
esportazioni |
valore della produzione |
|
settori venditori |
|
acquisti |
acquisti |
acquisti |
C |
G |
I |
E |
X |
|
A |
vendite |
0 |
4 |
4 |
5 |
5 |
3 |
2 |
23 |
|
B |
vendite |
6 |
0 |
4 |
3 |
4 |
4 |
3 |
24 |
|
C |
vendite |
2 |
6 |
0 |
10 |
5 |
5 |
2 |
30 |
|
salari |
W |
10 |
7 |
15 |
|
|
|
|
32 |
|
profitti |
V |
3 |
4 |
5 |
|
|
|
|
12 |
|
importazioni |
M |
2 |
3 |
2 |
|
|
|
|
7 |
|
valore della produzione |
X |
23 |
24 |
30 |
|
|
|
|
|
Il PRODOTTO
INTERNO LORDO dell’area urbana (Y) è dato dalla somma di SALARI (W) e PROFITTI
(V), ossia
Y = S W + S V
nell’esempio:
Y = 32 + 12
= 44
Il PRODOTTO
INTERNO LORDO dell’area urbana (Y) può altresì essere espresso come segue:
Y = S DOMANDA FINALE (C, G, I, E) – importazioni (M)
nell’esempio:
Y = (5 + 5
+ 3 + 2) + (3 +4 +4 + 3) + (10 + 5 + 5 +2) - 7 = 15 + 14 + 22 – 7 = 44
O, ancora,
Il PRODOTTO INTERNO LORDO dell’area urbana (Y) può essere espresso come segue:
Y = VALORE
TOTALE DELLA PRODUZIONE (X) – VALORE TOTALE DELLE IMPORTAZIONI (M) - S DOMANDA INTERMEDIA DEI SETTORI
nell’esempio:
Y = (23 +
24 +30) – (2 +3 +2) – [(0 + 4 + 4) + (6 + 0 + 4) + (2 + 6 + 0)] =
= 77 – 7 – [8 + 10 + 8] = 70 – 26 = 44
Entro questa matrice, prendendo in esame le
righe, ossia i RICAVI TOTALI DI OGNI SETTORE, ovvero il valore della PRODUZIONE
DI OGNI SETTORE, sono dati da:
X (A) = S acquisti settori intermedi + S acquisti della domanda finale
prendendo
come esempio il settore (A), si ha:
X (A) = (0
+ 4 + 4) + (5 + 5 + 3 + 2) = 23
Prendendo
in esame le colonne, ossia i COSTI TOTALI DI OGNI SETTORE, ovvero il valore
della PRODUZIONE DI OGNI SETTORE , sono dati da:
X (A) = S costi settori intermedi + salari + profitti +
importazioni
nell’esempio
del settore (A), si ha
X (A) = (0
+ 6 + 2 ) + (10 + 3 + 2) = 23
In una
economia chiusa, in cui non vi sono importazioni, esprimendo il valore Aij in proporzione al valore della produzione del settore
acquirente (X j) si ottengono i coefficienti tecnici aij,
ossia
aij = ![]()
nell’esempio,
il coefficiente tecnico del settore B nei confronti del settore A è dato da:
a ba
= ![]()
Esso
indica, ad esempio, quante lire di prodotto
dal settore B (venduto al settore A) sono necessarie per la produzione di 1
lira del settore A.
Conoscendo
i coefficienti tecnici dei vari settori costituenti la matrice e la domanda
finale è possibile pertanto determinare
il valore della produzione di ogni singolo settore,
Nell’ipotesi
di base dei modelli Input – output si suppone che i COEFFICIENTI TECNICI SIANO
COSTANTI all’aumentare della produzione e nel tempo.
Ciò implica
una ipotesi esplicita di assenza di RENDIMENTI DI SCALA.
Emerge
altresì una grande difficoltà ad utilizzare questi modelli a causa in genere
della mancanza di informazioni sui coefficienti tecnici a livello urbano.
Vengono talvolta impiegati per fare analisi in ambito regionale, ma anche qui
la mancanza di informazioni sui coefficienti
rendono questi modelli scarsamente usati.
VALUTAZIONI
CRITICHE SUI MODELLI DI BASE ECONOMICA
Il problema
principale che si incontra nell’uso di tutti i modelli di base economica urbana
è costituito dalla GENERALE CARENZA DI INFORMAZIONI QUANTITATIVE SULLA
CONSISTENZA DELLE ESPORTAZIONI URBANE.
Per
aggirare l’ostacolo si ricorre talvolta a semplificazioni analitiche del tipo:
si ipotizza che tutte le attività manifatturiere siano rivolte totalmente alla
esportazione e che le attività di servizio e l’industria delle costruzioni
siano invece rivolte a soddisfare la domanda locale, sia intermedia che finale.
Se tale semplificazione è ritenuta parzialmente accettabile per il settore
manifatturiero (dato che in genere la domanda locale non è sufficiente ad
acquistare tutta la produzione) non lo è spesso per i servizi (vedasi il caso
delle città d’arte, le capitali oggetto di turismo, ecc.).
Un altro
metodo utilizzato per stimare le esportazioni, allorquando si conosce il valore
delle produzioni settoriali, il valore aggiunto o la loro occupazione, è quello
denominato dei QUOZIENTI DI LOCALIZZAZIONE.
Esso
consiste nel CONFRONTARE la QUOTA DI OGNI SETTORE (Xic)
sul TOTALE DELLA PRODUZIONE URBANA LOCALE (Xc)
Sc = ![]() con la stessa QUOTA di
un’area di riferimento, ad esempio nazionale (Xn)
con la stessa QUOTA di
un’area di riferimento, ad esempio nazionale (Xn)
Sn = ![]() se il rapporto tra i
due QLi =
se il rapporto tra i
due QLi = ![]()
supera
l’unità, si considera la proporzione eccedente come espressiva di un surplus
netto rispetto alle esigenze della domanda locale.
Anche
questo metodo contiene forti limitazioni perchè
considera SIMILI LE STRUTTURE di DOMANDA LOCALE E NAZIONALE, non considera
l’esistenza di esportazioni nette nazionali.
Se
applicato all’occupazione implica l’assunzione di UGUALI LIVELLI DI
PRODUTTIVITA’ nello spazio.
LIMITI AL
PRINCIPIO DELLA BASE ECONOMICA URBANA
Il
principio della base economica urbana, nelle sue diverse versioni, nasce in un
contesto di analisi statica.
Se risponde
infatti al buon senso l’osservazione che una città tende a PROSPERARE quando
“tira” la DOMANDA dei prodotti della SUA SPECIALIZZAZIONE, e che al contrario
al venir meno di questa si genera CRISI, il modello formalizza in modo
ristretto questa affermazione ma tende anche ad estenderla su archi temporali
probabilmente incompatibili con la rigidità delle sue ipotesi di base.
Le versioni
AGGREGATE del modello possono presentare precisi limiti proprio a causa di tale
aggregazione dato che la crescita della domanda di un certo settore di “base”
può indurre uno sviluppo completamente diverso dalla crescita della domanda di
un altro settore di specializzazione.
Il modello
ipotizza che non vi siano “strozzature” dal lato dell’OFFERTA che limitino la
crescita dei settori locali e che pertanto esistano capacità produttive non
utilizzate, fattori produttivi non occupati o possibilità di espansione a costo
zero.
Nel più
lungo periodo il modello si scontra col problema della STABILITA’ DEI
MOLTIPLICATORI. E’ noto infatti che col crescere della città cresce anche la
quota delle attività non di base che incidono appunto sul moltiplicatore.
Nel lungo
periodo mutano anche altri elementi su cui si fonda il modello: la capacità
competitiva dei settori di specializzazione, la specializzazione stessa della
città.
Se si
mantengono inalterati i rapporti di competitività dei settori di
specializzazione fra diverse città, per focalizzarsi esclusivamente sui tassi
di crescita della domanda nazionale o internazionale dei settori di rispettiva
specializzazione, significa obbligarsi a trascurare ciò che vi è di più
rilevante nei PROCESSI DI SVILUPPO: IL CAMBIAMENTO STRUTTURALE.
L’ANALISI
SHIFT – SHARE
Per cercare
di contenere i limiti ai modelli sopra accennati, si sono cercate alcune
strade.
L’analisi
“shift – share” scompone il TASSO DI SVILUPPO DIFFERENZIALE di un’AREA LOCALE (Xc) rispetto ad un SISTEMA DI RIFERIMENTO (Xn), ad esempio nazionale
Xc – Xn
in due effetti:
·
l’effetto di
COMPOSIZIONE (MIXc)
·
l’effetto di
COMPETIZIONE (DIFc)
la somma di
questi due effetti dà, per definizione, il tasso di sviluppo differenziale
dell’area in esame rispetto al sistema di riferimento, ossia:
MIXc + DIFc = Xc –Xn (1)
L’EFFETTO
DI COMPOSIZIONE nasce dalla forte presenza nell’economia locale di quei settori
che a livello nazionale mostrano una DINAMICA PIU’
ACCENTUATA, e cioè che presentano UNA DOMANDA RAPIDAMENTE CRESCENTE.
Se
indichiamo con
·
X la variabile osservata (valore aggiunto,
occupazione);
·
con gli indici “c”
il riferimento alla città e con “n” il riferimento alla nazione;
·
con gli indici “ic” il riferimento al settore della città e con “in”
il riferimento al settore nazionale;
·
l’apice “°”
l’anno di riferimento e con “1” l’anno di osservazione
l’effetto di composizione MIXc è dato da
MIXc = 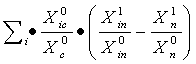
l’effetto
di competizione DIFc è dato da:
DIFc = 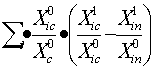
ovvero
anche, ricavato dalla (1)
DIFc = Xc
– Xn - MIXc
Nei termini
dell’analisi shift – shar, ipotizzare che la
componente MIX settoriale sia PIU’ RILEVANTE dello sviluppo locale, significa che
dovrebbero crescere più delle altre, quelle città che sono specializzate nei
settori più dinamici a livello nazionale, ossia quelli che prevedono una
domanda più vivace facendo però assumere all’effetto di competizione un ruolo
residuale.
Anche questa
ipotesi sembra non rispondere adeguatamente ai cambiamenti che si sono
osservati: infatti assai frequentemente
si rileva che la domanda nazionale scende in secondo piano rispetto al
dinamismo specifico dell’offerta locale prodotto dalla specifica capacità
competitiva locale.
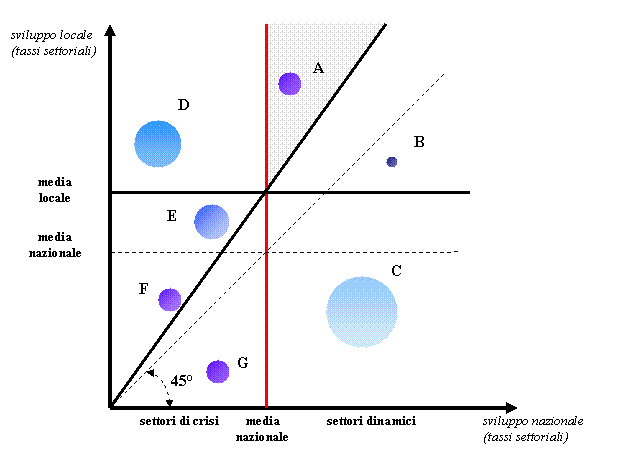
Quanto
sopra detto può essere schematizzato su un piano cartesiano in cui sull’asse
delle ascisse (x) vengono posti i TASSI DI SVILUPPO SETTORIALI NAZIONALI mentre
sull’asse delle ordinate (y) vengono posti
TASSI DI SVILUPPO SETTORIALI LOCALI. Ogni settore viene rappresentato da
un punto sul piano cartesiano
|
|
Fig.5.3
Si osserva
che:
a – un
effetto MIX FAVOREVOLE nasce da una forte presenza nell’economia loca le di
settori che ricadono nella parte DESTRA del grafico (settori A – B- C );
b – un
effetto DIF FAVOREVOLE nasce dalla collocazione prevalente dei diversi settori
locali al DI SOPRA DELLA LINEA TRATTEGGIATA INCLINATA DI 45° (settori A – D – E
–F);
c – I
SETTORI CHE GIACCIONO SOPRA LA LINEA CONTINUA (che può stare al di sopra o al
di sotto della linea tratteggiata a seconda che il tasso di sviluppo
complessivo dell’area locale sia superiore o inferire a quello nazionale), sono
i settori in cui esiste un VANTAGGIO COMPARATO
dell’area in esame (settori A – D- E – F);
d – la
migliore condizione urbana è collegabile ad una forte presenza di settori che
si collocano nel quadrante A (settori dinamici) o anche nel quadrante B (con
dinamica locale più debole, ma sufficiente a mantenere un elevato sviluppo
complessivo);
e – una
condizione favorevole può anche derivare da una SPECIALIZZAZIONE in settori che
sono sì “tradizionali” o “di crisi”, come i settori D o E, ma in cui la forte
competitività locale genera elevati tassi di sviluppo. In questo caso la
crescita ridotta della domanda nazionale non riuscirebbe a spiegare il successo
locale;
f – una
specializzazione in settori che cadono nel quadrante C in cui la domanda
nazionale è elevata ma la competitività locale è assai scarsa, rende fuori
gioco un modello di base di esportazione come strumento di previsione dello
sviluppo;
g – una
specializzazione in settori del tipo F o G farebbe invece facilmente diagnosticare
una crisi rilevante.
IL RUOLO
DEI SERVIZI
Si è visto
che una buona performance locale non può essere basata solo sulla crescita
della domanda esterna.
Circa il
ruolo dei servizi nello sviluppo locale si sono formate opinioni e teorie
diverse, tra chi sostiene che sono proprio i settori non di base a determinare le performace
locali di lungo periodo dato che essi sono generatori di qualità e chi al
contrario ritiene che pur in presenza di una qualificata e forte struttura dei
servizi, di fronte ad un crollo della domanda mondiale degli altri settori, la
crisi di questi sarebbe inevitabile.
Al di la là
di queste estremizzazioni, è fuori discussione il fatto che la presenza in un
territorio di qualificate strutture dei servizi concorre a generare quelle
flessibilità e capacità di adattamento dell’economia locale che stimola una
continua capacità di rapida sostituzione dei settori con domanda in declino con
altri più moderni e dinamici.
Si osserva
infatti che la competitività di una città non è certo toccata dalla presenza di
sofisticate botteghe di salumeria o di sale cinematografiche, bensì dalla
presenza di centri universitari, di centri di eccellenza tecnologica.
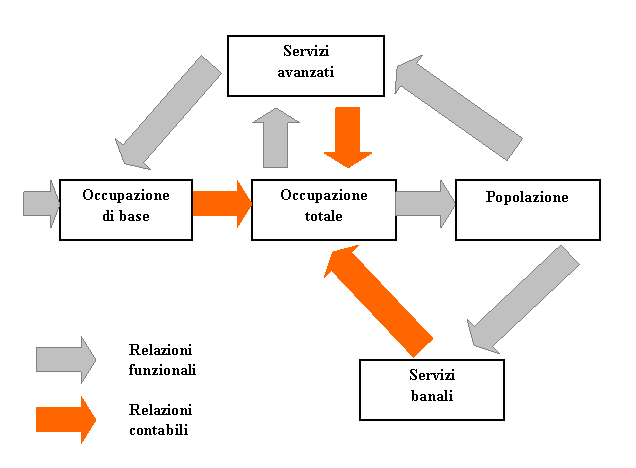
Si sono
pertanto costruiti dei modelli di base di esportazione integrati con i servizi.
La logica
di questi modelli è rappresentata dalla figura:
|
|
ed è la
seguente: una crescente dimensione dell’OCCUPAZIONE e della POPOLAZIONE urbana
genera la nascita di servizi avanzati qualificati e questi a loro volta
interagiscono con l’occupazione di base consentendole di rinnovare la
competitività e la composizione settoriale interna.
I MODELLI
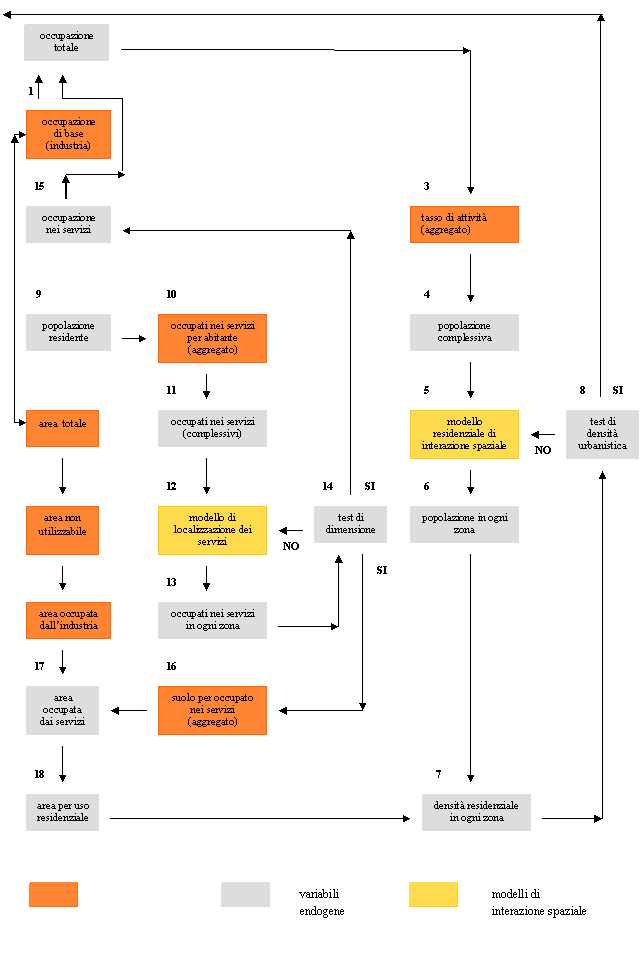
GENERALI DI SVILUPPO URBANO E USO DEL SUOLO
I modelli
sino ad ora illustrati considerano la città come un’unità aggregata in senso
spaziale e non riescono a spiegare la strutturazione interna della città, delle
sue zone.
Per tentare
di fornire modelli per la programmazione del territorio sono stati elaborati
altri tipi di modelli detti MODELLI GENERALI.
Tali
modelli simulano la struttura interna della città, la sua evoluzione in periodi
successivi e distinti, la localizzazione delle diverse attività, la loro
interazione e la conseguente domanda di trasporto.
Il
capostipite di questi modelli è quello di LOWRY (1964)
IL MODELLO
DI LOWRY
Il modello
si propone di simulare la struttura degli usi del suolo urbano in un dato
momento sulla base di un limitato numero di informazioni:
·
l’entità e la
localizzazione delle attività industriali nella città
·
la matrice delle
distanze e dei tempi di trasporto fra zona e zona.
Il modello
stima:
a – la dimensione della
popolazione urbana totale e la sua localizzazione nelle “n” zone in cui è
ripartita la città;
b – la dimensione
dell’occupazione di servizio alla popolazione e la sua localizzazione nelle
zone;
c – il pattern (modello,
schema) degli spostamenti casa-lavoro e casa–negozio e, pertanto, la domanda
complessiva di trasporto nella città.
Anche
questo modello ha il difetto di simulare una ISTANTANEA della metropoli dato che il riferimento sono
le variabili esogene del modello (in particolare l’occupazione delle attività industriali
e la loro localizzazione).
L’ipotesi
sottostante alla parte localizzativa del modello è
quella che vede la scelta RESIDENZIALE come guidata da SOLE considerazioni di
ACCESSIBILITA’ AI LUOGHI DI LAVORO e la scelta di localizzazione dei servizi determinata
a sua volta da queste considerazioni.
L’OCCUPAZIONE
TOTALE (Lt) è data dalla somma dell’occupazione di
BASE INDUSTRIALE (Lb) e di quella di SERVIZIO (Ls).
Lt = Lb + Ls
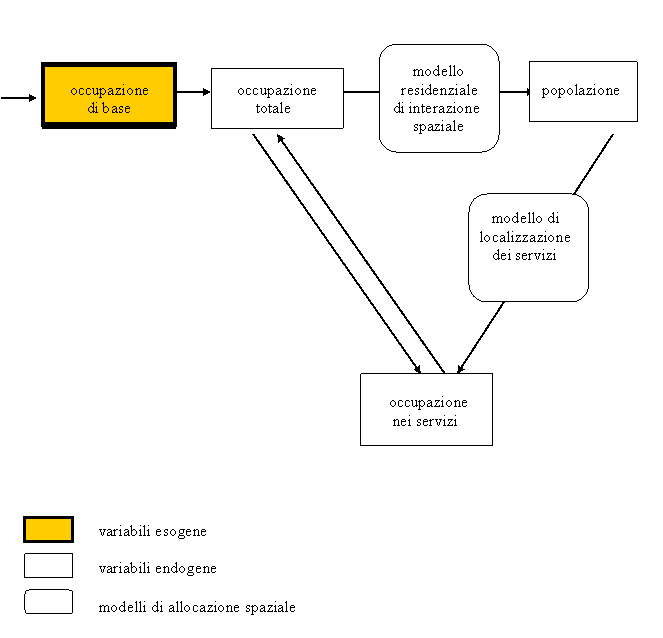
L’occupazione
totale genera, attraverso il tasso di ATTIVITA’, la DIMENSIONE della
POPOLAZIONE e questa a sua volta genera, tramite una serie di coefficienti di attivazione di OCCUPAZIONE DI SERVIZIO PER
PERSONA RESIDENTE, l’OCCUPAZIONE DI “K”
SETTORI DI ATTIVITA’ SERVIZIO.
La
distribuzione territoriale di quest’ultima variabile
è determinata dalle LOCALIZZAZIONI RESIDENZIALI ed in parte anche dalla
LOCALIZZAZIONE DELL’OCCUPAZIONE TOTALE.
La logica
operativa dell’intero modello è schematizzata nel diagramma a flussi seguente.
Anche i due
modelli di interazione spaziale utilizzati da Lowry e
che chiamano MODELLI DI POTENZIALE non danno risposte soddisfacenti ed il loro
impiego non è mai entrato nella prassi urbanistica corrente, almeno in Italia.
BIBLIOGRAFIA
1 - Roberto Camagni, Principi di economia urbana e territoriale,
Carocci editore.
start variabili esogene 2 start
![]()